a libc qsort() shootout of sorts
The C Standard Library (libc) provides a generic sort function called qsort(). While the q prefix suggests that quicksort might be a good choice of algorithm, the standard does not dictate what algorithm an implementation should use.
In this post we’ll take a look at a few libc qsort() implementations and try to contrast their performance.
What to measure?
Evaluating an implementation’s performance by measuring execution time won’t work. Some of the C libraries we’re interested in are proprietary and can only be run on specific hardware with a specific operating system. Other libraries target particular types of hardware, e.g. embedded, or are written to work well with a particular compiler’s optimization strategy. Run time on one specific combination of operating system, hardware and compiler, is not a very useful metric.
A nice property of qsort() is that it is a generic sort function, meaning it can sort any type of data. The order and how to compare elements is defined by a comparison function which the caller must pass to qsort(). Since we control the comparison function, we can also count how many comparisons an implementation performs.
We claim that this, the number of comparisons, is a pretty good metric. Invoking the comparison function is a fairly heavy operation, so the less often it is invoked the better. This is especially true when comparisons are expensive, e.g. when sorting long strings or complex data structures.
It could also be that this is a stupid metric, but whatever.
The combatants
We’ve a total of 14 different sort functions to go through. The not-very-interested reader can skip ahead to the results and fancy graphs below.
GLIBC
The GNU project’s libc implementation, GLIBC, powers most GNU/Linux distributions (sometimes in the shape of EGLIBC) and several other operating systems. This qsort() is interesting in that it shuns quicksort in favour of merge sort. Unlike quicksort, merge sort is not in-place and requires at least \(O(n)\) additional memory. If that memory is not available, or if it exceeds a fourth of the machine’s physical RAM, then GLIBC will fall back to an in-place quicksort. The quicksort in turn resorts to insertion sort for arrays of 4 or fewer elements.
In the graphs below, the merge sort and quicksort implementations have been separated: glibc-2.17_merge and glibc-2.17_quick respectively. Our humble gut feeling is that the merge sort is what most commonly runs in “production” and that it is the most representative of the two for GLIBC. YMMV.
BSD
FreeBSD qsort() is a quicksort based on Engineering a Sort Function by Bentley and McIlroy. A significant deviation from the paper is that the BSD qsort() doesn’t only resort to insertion sort for small arrays, but also does so whenever a partitioning round is completed without having moved any elements. The latter is intended to capture nearly sorted inputs, since insertion sort will handle these cases in linear time.
The implementation appears to have undergone very little change since the days of 4.4BSD Lite and is essentially identical to that of OpenBSD and DragonflyBSD. It is also appears in newlib and probably also in OSX.
NetBSD
NetBSD’s qsort() used to be identical to that of the other BSDs but as of version 6.0 the aforementioned deviation from Bentley and McIlroy has been removed. In other words, NetBSD qsort() does not switch to insertion sort when a partitioning round finishes without moving elements.
The motivation for this change seems to be the possibility of particular inputs triggering insertion sort in spite of the data being highly unsorted. This in turn would mean quadratic complexity, which can be devastating for large inputs. The issue has been discussed by FreeBSD hackers earlier.
klibc
When a machine running Linux is booting and the kernel has just been brought up, klibc is made available to allow certain early user space programs to operate in spite of not yet having access to a “real” C library. Klibc is designed to be as small and as correct as possible and is sometimes mentioned as a good fit for embedded systems. At roughly 40 lines of C, the qsort code is very compact and easy to grok.
The klibc qsort() implements the comb sort algorithm; a bubble sort on steroids. The source code claims a time complexity of \(O(n\log n)\) but there is a lot of conflicting information floating around. Vitányi put the average complexity at \(\Omega(n^2/2^p)\), where \(p\) is the number of passes, but to what extent that matters in practice is not clear.
uClibc
Originally created to support uClinux, a linux distribution targeting embedded devices and micro-controllers, the uClibc is designed to “provide as much functionality as possible in a small amount of space”.
This qsort() implements shellsort which, similarly to the comb sort of klibc, is an insertion sort on juice. The time complexity depends on the “gap sequence” used, which in uClibc’s case is the \((3^k-1)/2\) (for \(k=1,2,\ldots\)) sequence suggested by Knuth. This puts the algorithm at \(\Theta(n^{3/2})\). There are other more efficient sequences out there but Knuth’s sequence is both compact and simple in implementation.
dietlibc
The diet libc is designed to be as small as possible. Its qsort() is a compact and straightforward quicksort without many bells and whistles. There is no switch to a low overhead algorithm for small arrays and only a single element is sampled when choosing pivot.
It is worth mentioning that dietlibc 0.32 used to always select the last element as pivot. This results in qsort() using \(O(n)\) stack frames for sorted inputs, effectively crashing due to stack overflow on anything but tiny numbers of elements. This has been fixed in 0.33 by choosing random pivots and that is also the version we consider in this article.
musl
Smoothsort is a variation of heapsort that performs especially well on nearly sorted inputs. It’s a pretty complicated beast and it does take some effort to wrap one’s head around it. Keith Schwarz has posted a nice walkthrough that the interested reader should check out.
Considering that musl libc puts simplicity among its design goals, the choice of smoothsort could seem odd. The code is however clean and readable and getting an \(O(n\log n)\) worst case with near linear complexity for nearly sorted inputs is a pretty sweet deal.
illumos
OpenSolaris ceased to exist in 2010 after Oracle bought Sun Microsystems. A fork of the project lives on in the shape of illumos and OpenIndiana. The distinction between the two is a tad fuzzy but the C library appears to be part of illumos.
This qsort() is very well commented and should serve nicely as a starting point for anyone interested in studying the quicksort algorithm. It samples multiple elements for pivot and switches to insertion sort for small partitions.
plan9
Last but not least among the free software libraries, we have Plan 9 from Bell Labs. This research OS was/is developed as a successor to Unix. It’s worth reading up on.
Plan9’s qsort() is a very clean looking quicksort, although it wouldn’t have hurt to throw in a comment or two in the code. It does not switch to a low overhead algorithm for small inputs/partitions, but it does sample multiple elements when choosing its pivot.
proprietary C libraries
We’ll also have a look at the performance of a couple of proprietary qsort() implementations. The source code for some of these is surely floating around on the intrawebs, but since they’re non-free we won’t discuss them in detail.
- IRIX 6.5 on an Origin 300
- OpenVMS 8.3 on a DEC AlphaStation 200 4/166
- Visual Studio 2005 on x86 running Windows XP
- Solaris 10 on x86
Many thanks to andoma for providing the VS2005 data. Many many thanks to njansson for providing access to his SGI machine, his VAX cluster and to his x86 Solaris server.
Results
Random data
We’ll start by looking at the number of comparisons when sorting random data.
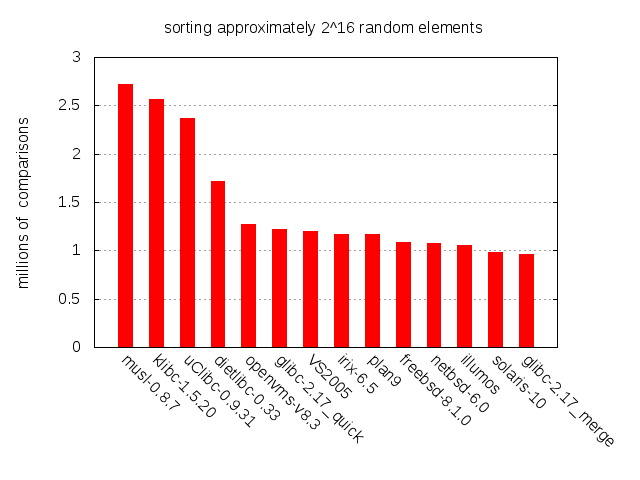
The slightly less orthodox algorithms - musl’s smoothsort, klibc’s comb sort and uClibc’s shellsort - can be found on the left hand side. These are followed by dietlibc’s somewhat naive quicksort implementation.
Further right we find the C libraries of, or associated with, more or less major operating systems. It may be pointless to try to draw any conclusions about how these fair against each other - they’re all doing pretty well - but we can still discern three clusters.
The most well performing one holds GLIBC’s merge sort and the proprietary qsort() of solaris 10. To the least well performing we count OpenVMS, VS2005, IRIX, plan9 and GLIBC’s quicksort. The BSD quicksorts, both with and without the heuristic for switching to insertion sort for nearly sorted data, and illumos reside in the middle.
What happens when we bump up the input size by a factor of 64?
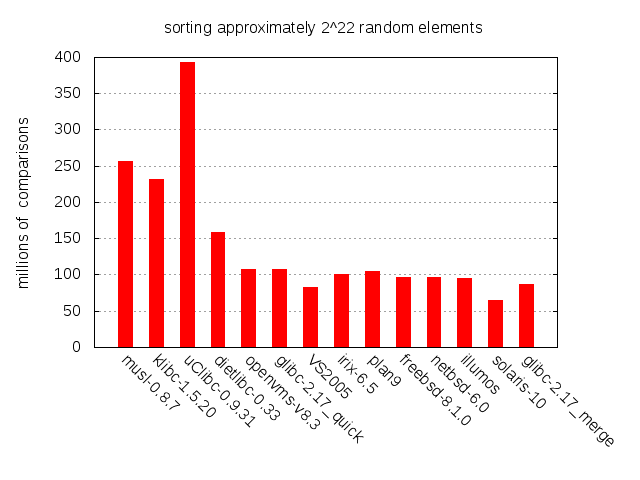
There’s a distinct improvement for VS2005 and especially for Solaris
- They are definitely doing something right, but being non-free software, it’s hard to say exactly what. uClibc, on the other hand, doesn’t appear to scale very well at all. This trend is perhaps more clear as we plot the number of comparisons for multiple input sizes.
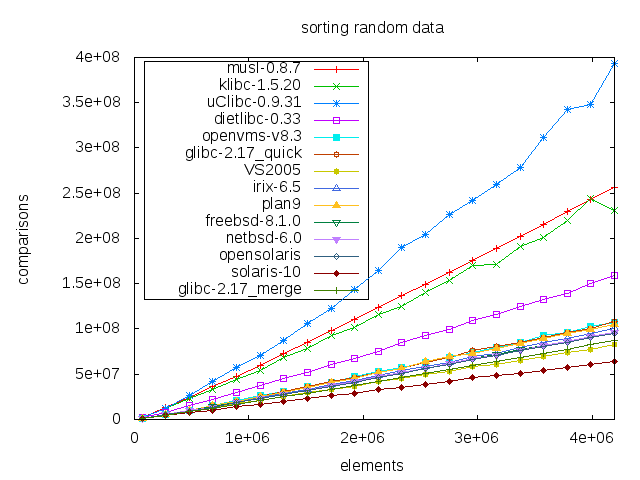
Ordered data
While random data may seem like the most important test case, it is also important to consider nearly or completely sorted inputs. We should be able to expect nice behaviour from FreeBSD, with its switch to insertion sort for nearly sorted data, but not so much from NetBSD which removed said switch. Musl libc’s smoothsort should also behave nicely for these inputs.
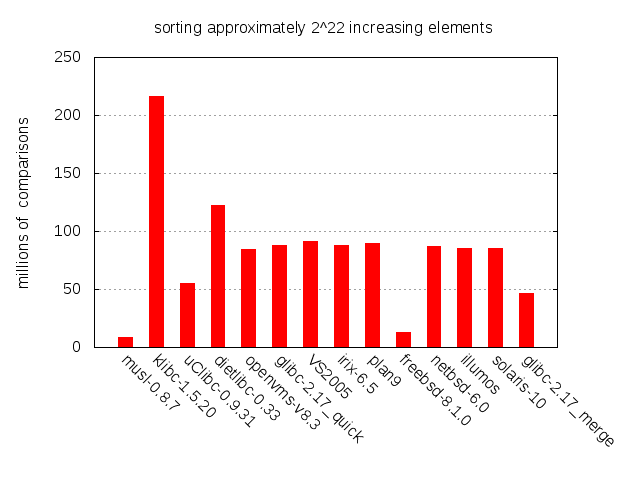
As expected, both FreeBSD and musl libc perform very few comparisons in this case. We also see that uClibc’s shellsort is doing quite well. Given the shellsort algorithm’s basis in insertion sort, which is great for sorted inputs, this is not too surprising. The merge sort of GLIBC also deserves mention.
Finally, we’ll have a look at what happens when sorting strictly decreasing input, i.e. the reverse of sorted input.
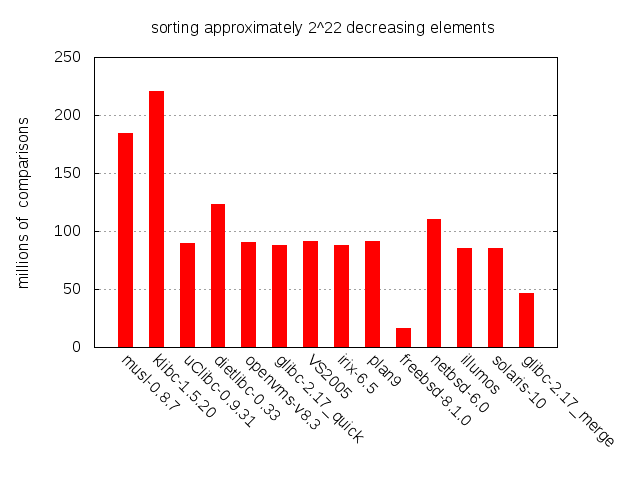
Here we see a drop in performance for musl, uClibc and NetBSD. FreeBSD however remains the same. As it turns out, FreeBSD’s strong performance on decreasing data stems from how the quicksort partitioning round is implemented. It mostly reverses the order of the elements in each partition, which in turn allows the heuristic for nearly sorted data to kick in early. Is this intentional or just a happy accident? No idea.
Does this matter?
Previously we argued that the number of comparisons is a useful metric. If nothing else, it allows us to reason about the relative performance of proprietary implementations running on archaic/obscure hardware (no offense to fans of SGI or VAX). But how strong is the correlation between this metric and actual performance?
In the bar chart below we find actual execution time in seconds side by side with the number of comparisons for all the free software implementations. This data was gathered on a Lenovo X220 running Debian GNU/Linux. Compilation was done with gcc 4.4.5 using optimization level 0 (-O0).
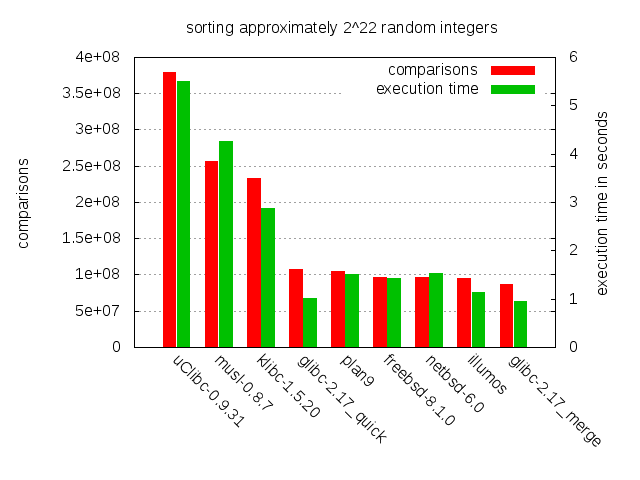
Again, we’re not really interested in which implementation happens to be the fastest on our particular combination of hardware, OS and compiler, but it is pleasant to note that this data doesn’t completely contradict the hypothesis of the number of comparisons being a reasonable metric.
That was all. Over and out.