algorithmic complexity attacks and libc qsort()
An algorithmic complexity attack is a denial of service attack that triggers worst case behaviour in code that is otherwise expected to perform well. The canonical example would be the widely published attacks against hash table implementations, where carefully crafted inputs made snappy \(O(1)\) operations deteriorate into \(O(n)\) time sinks. Several major programming language implementations and web frameworks were vulnerable.
Quicksort is also commonly mentioned in this context. Its expected \(O(n\log n)\) and worst case \(O(n^2)\) makes it a prime candidate. When we previously looked at libc qsort() implementations it became clear that while many different algorithms are in use, quicksort is by far the most common choice. This is so for good reasons. In addition to the average-case complexity, quicksort is cache friendly and optimizes well.
In this post we’ll have a look at how to trigger worst case performance in a couple of libc qsort() implementations.
Breaking BSD
Inspecting a diff between the qsort() of 4.4BSD-Lite and that of current day FreeBSD reveals that very little has changed since 1994. Some K&R syntax has been removed, some macros have been introduced, support for the reentrant qsort_r() has been added and a couple of variables have been renamed. Other than that, the code is pretty much the same.
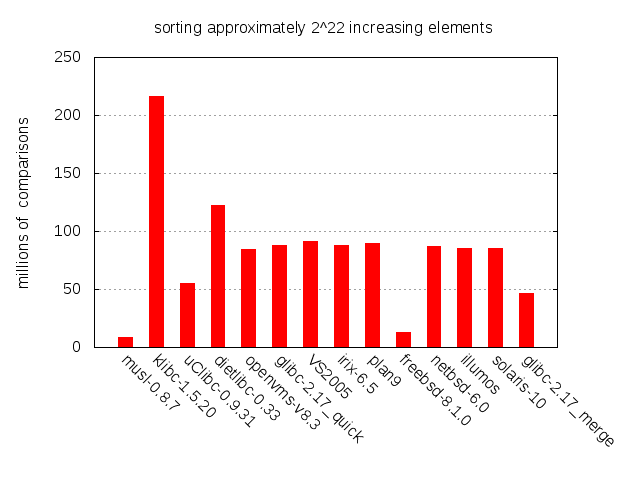
This isn’t a cause for concern in and of itself. As we saw in the previous post, the implementation performs very well and appears to have stood the test of time. It is particularly good on partially sorted inputs, which are commonly encountered in practice. In the chart above it outperforms several other major C libraries. We’ll soon discuss why, but first a little background on quicksort and how BSD has implemented it.
Quicksort 101
The basic flow of quicksort is as follows:
- Select a pivot element
- Partition the data around the pivot; smaller elements to the left, larger to the right
- Recursively quicksort each partition
As long as the partitions end up being of roughly the same size, we can expect the algorithm to run in \(O(n\log n)\). An ideal pivot selection would always pick the median element, since that produces perfectly balanced partitions. The worst possible pivot selection is that which results in highly skewed partitions; the goal of each round is not to merely shave off a few elements, the goal is to split the problem in half.
Selecting the true median in each round of partitioning is unfortunately prohibitively expensive. It can be done in linear time but the constant factors are just too high for this to make any sense in practice. BSD qsort() approximates the true median by sampling up to 9 elements, like so:
pivot = median(median(v[0], v[n/8], v[n/4]),
median(v[n/2 - n/8], v[n/2], v[n/2 + n/8]),
median(v[n-1 - n/4], v[n-1 - n/8], v[n-1]))
Like most of the BSD quicksort, this pivot selection is based on Bentley and McIlroy’s Engineering a Sort Function. This paper covers many of the less obvious aspects of how to implement quicksort. Well worth a read if you’re into the whole sorting thing.
When a partition or an original input is sufficiently small, it can pay off to switch to a low overhead algorithm. In the BSD case, this algorithm is insertion sort and it is chosen whenever \(n\lt 7\). While the time complexity of insertion sort is quadratic, its low constant factor makes it really shine on such small inputs. Now this is all well and good, but BSD goes one step further.
The BSD deviation
As mentioned before, the BSD qsort() outperforms its competition on sorted and partially sorted inputs. This is due to a pretty simple heuristic: whenever a partitioning round finishes without rearranging any elements, we switch to insertion sort! In other words, whenever an input is perfectly partitioned around the approximated median, BSD qsort() assumes that the input is nearly sorted and pulls the insertion sort trigger. Insertion sort in turn, while quadratic in the worst case, is in fact linear on nearly sorted inputs, so excellent performance can be expected.
As it turns out, this heuristic also opens up for a very nasty worst case behaviour. Consider an input created by the following snippet of code:
for (i = 0; i < n/2; i++) v[i] = n/2 - i;
v[n/2] = n/2 + 1;
for (i = n/2 + 1; i < n; i++) v[i] = n + n/2 + 1 - i;
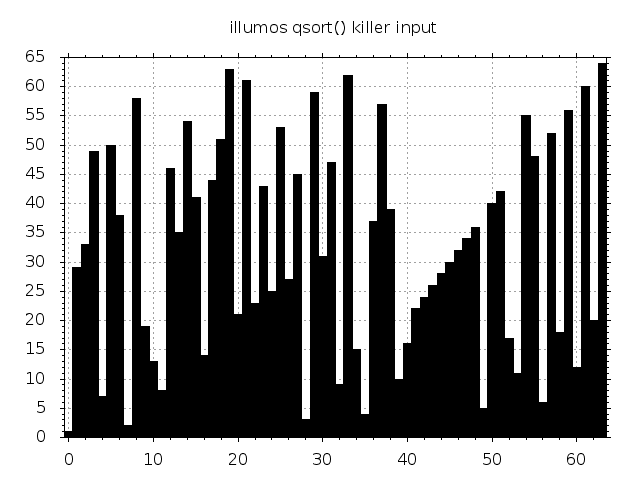
The plot below visualizes this input for \(n=64\).
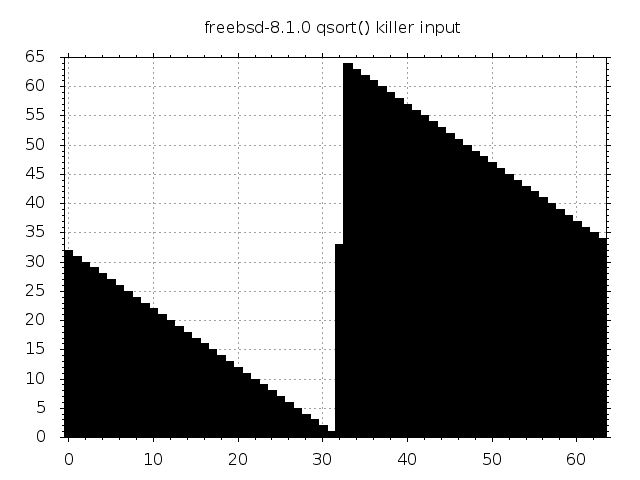
Feed this into the BSD pivot selection and the element at position \(n/2\) will pop out. Since the data is already perfectly partitioned around this element, no other elements will be rearranged, qsort() will assume that it’s facing a nearly sorted input and will switch to insertion sort. The data is however far from sorted and the algorithm will exhibit catastrophic quadratic behaviour.
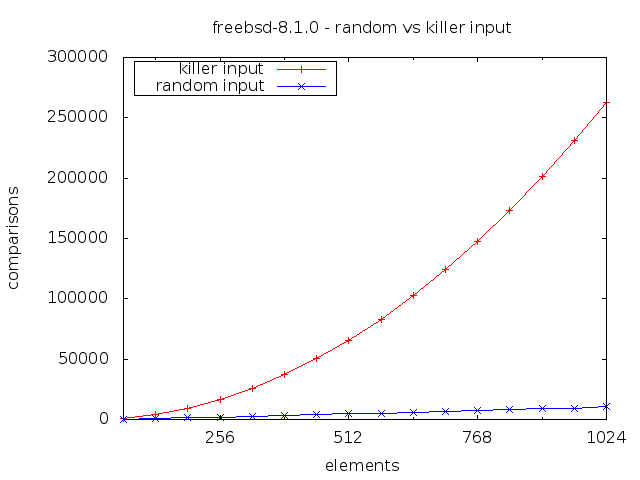
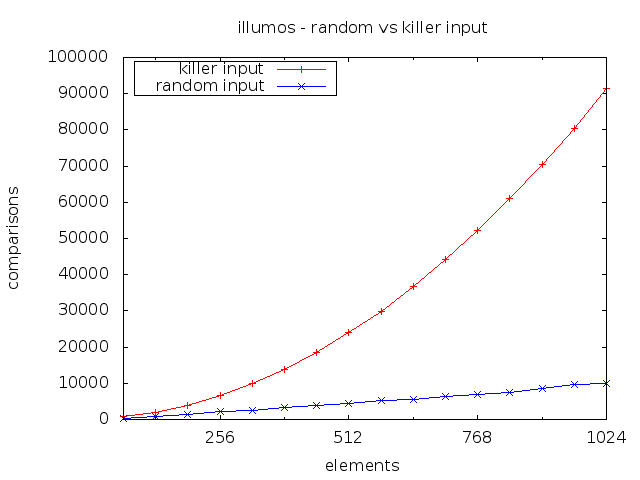
Notice how doubling the input size roughly quadruples the number of comparisons performed. This is of course the trademark of an \(O(n^2)\) algorithm.
4.4BSD-Lite has many descendants and both OpenBSD (5.5) and DragonflyBSD (3.8.0) seem to behave exactly like FreeBSD on these inputs. Many other software projects, both free and proprietary, have also incorporated this implementation. But not NetBSD! A 2009 commit removed the switch to insertion sort, citing “catastrophic performance for certain inputs”. Similar modifications can be found in e.g. PostgreSQL and OSX.
Breaking almost any quicksort
The same McIlroy who co-authored Engineering a sort function (the article mentioned above; the one you should read) also wrote A Killer Adversary for Quicksort. In a nutshell, this article describes a simple adversarial program, antiqsort, which reduces almost any quicksort implementation to quadratic performance. If an implementation is susceptible, then simply linking against libc and running once is sufficient to produce a worst case input. But there’s no point in rehashing the article - it really is both well-written and accessible - so let’s instead have a look at what antiqsort can do to the NetBSD qsort().
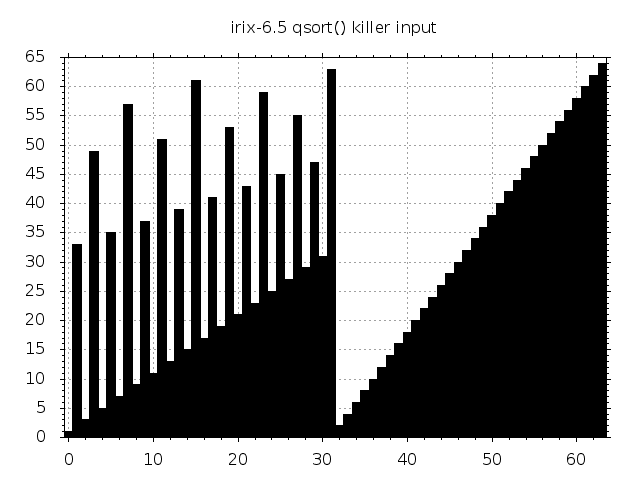
McIlroy vs NetBSD
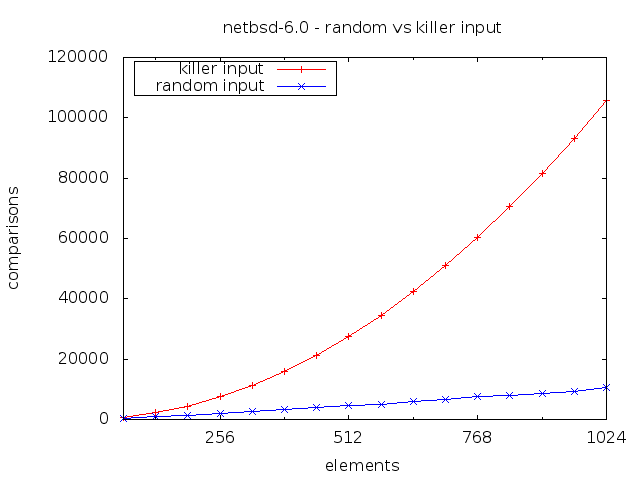
Blam! Quadratic complexity. The absolute numbers aren’t quite as bad as for the regular BSD qsort(), but it is quadratic and that’s bad enough.
The visualization of the FreeBSD killer input was inspired by similar graphics for Digital Unix in McIlroy’s article. As it turns out, the corresponding visualization for NetBSD is not even remotely as pretty.
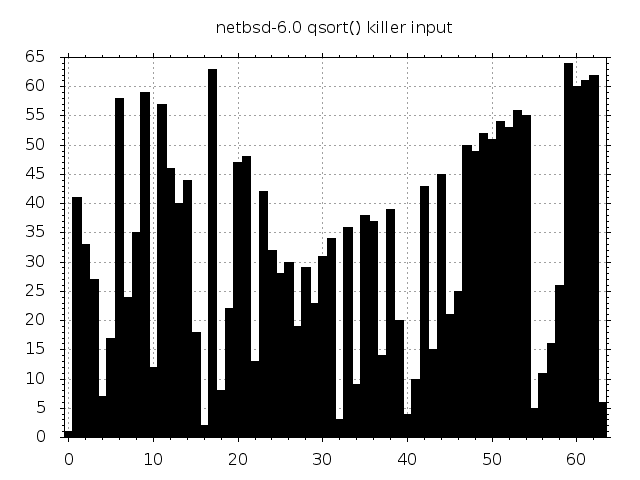
Good looks are however of no consequence here. McIlroy’s adversary can generate these inputs of any size for (almost) any quicksort just by linking and doing a single round of sorting. The only caveat is that if the implementation is randomized, then we lose the ability to “replay” the input at a later time. Again, not a big problem in practice since very few C libraries bother with randomization of their sort function.
McIlroy vs the world
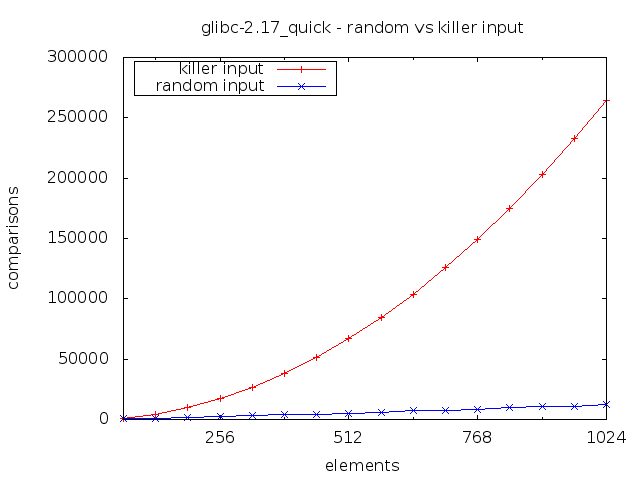
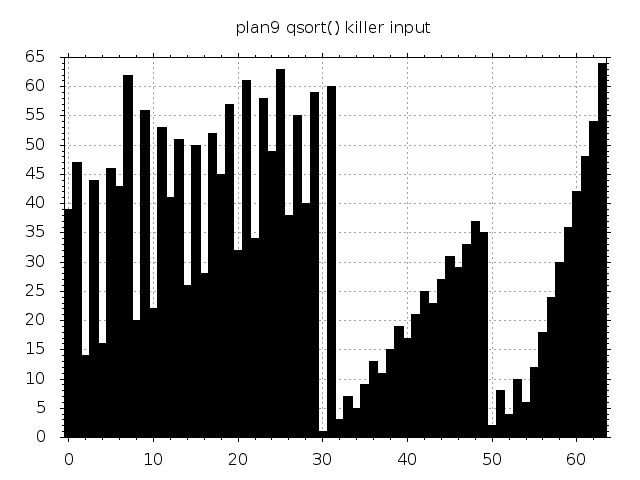
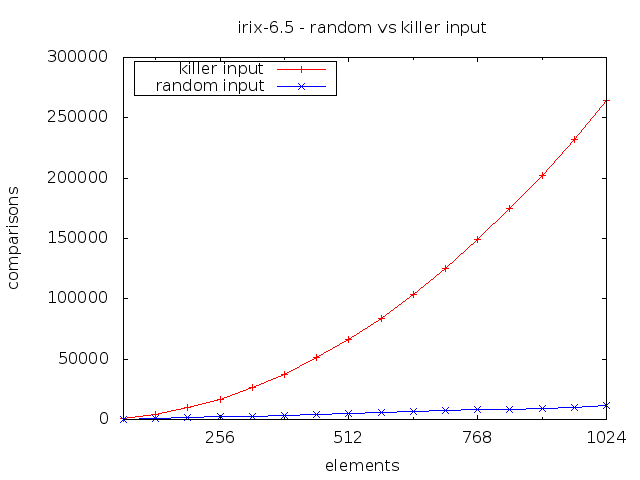
Let’s have a look at how the McIlroy adversary fares against a couple of other libc quicksort implementations. Bear in mind that quicksort is not the default code path of glibc qsort(). It prefers using mergesort and only falls back to quicksort when certain memory limits come into play. More on that and on the other implementations in the previous post.
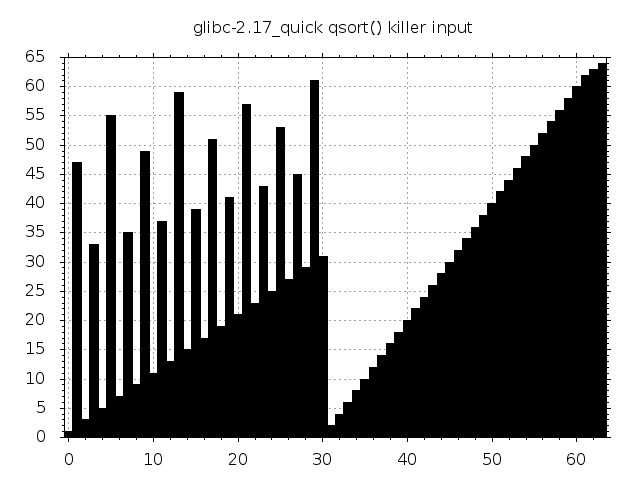
|
|
|

|
|
|
|
|

|

|
Some inputs are beautiful. Some aren’t. They all trigger quadratic complexity.
Can this be exploited?
If this was such a big deal then we would probably be seeing algorithmic complexity attacks against qsort() all the time in the wild. And we don’t. Very few programmers would willingly call qsort() on untrusted user input. This is not even remotely as serious as the previously mentioned hash table attacks.
With that said, calling the BSD qsort() on a 216 killer input is about 1000 times slower than on a random input of the same size. Most benchmarks are unlikely to test such an edge case so it is at least conceivable that this vector might some day be exploited in a denial of service attack.
A “real world” example
One example of a potential real world issue lies in how some software implements directory listings. It is common to order directory entries by e.g. name or timestamp and it is common to create that ordering by calling qsort(). This applies to many implementations of the venerable ls(1) utility as well as the autoindex functionality of some web servers.
To exploit this we need the ability to create files and the ability to control the order in which directory entries are read (e.g. by means of readdir(3) or fts_read(3)). The latter is simplified by BSD’s Unix File System (UFS), where directory entries are effectively returned in the order that they were created. Here’s the time consumption for listing 215 random entries on a FreeBSD 9.1 box:
$ time ls -1 random/ > /dev/null
real 0m0.065s
user 0m0.022s
sys 0m0.004s
Very snappy and unlikely to cause any concern in a benchmark. Let’s see what happens when we create and list a killer input of the same size:
$ mkdir killer
$ for i in $(seq -w 16384 1); do touch killer/$i; done
$ touch killer/16385
$ for i in $(seq -w 32768 16386); do touch killer/$i; done
$ time ls -1 killer/ > /dev/null
real 0m5.866s
user 0m5.719s
sys 0m0.006s
A pretty dramatic performance drop and almost exactly what we would expect. If the 216 killer results in a factor 1000 drop, then 215 should give about factor 250. Here we saw a drop from 0.022s to 5.719s user time, so factor 260 slower.
Whether or not an attack based on this approach can actually be carried out in the wild is a question that we leave unanswered. The ability to create arbitrarily named files is typically reserved for trusted users, so perhaps not.
TL;DR
Plain BSD qsort() can easily be tricked into running insertion sort on its whole input with terrible performance as a consequence. There exists a simple technique for triggering similar behaviour in almost any quicksort implementation, including those of most major libc implementations. Exploiting this in an algorithmic complexity attack in the wild is likely not trivial but is under certain circumstances conceivable.
That was all. Over and out.
See also: Discussions on hacker news and proggit