brainfuck optimization strategies
In almost every computation a great variety of arrangements for the succession of the processes is possible, and various considerations must influence the selection amongst them for the purposes of a Calculating Engine. One essential object is to choose that arrangement which shall tend to reduce to a minimum the time necessary for completing the calculation.”
Ada Lovelace, 1843
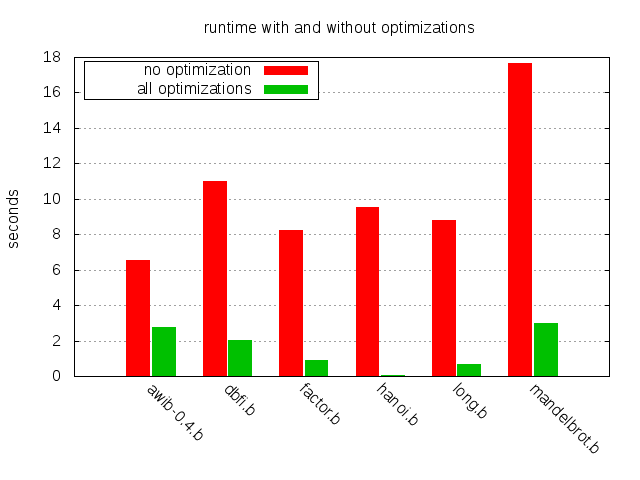
Lovelace’s words still ring true, almost two centuries later. One way to choose that arrangement is to use an optimizing compiler. In this post, we’ll have a look some important compiler optimization strategies for the brainfuck programming language and we’ll examine how they affect the run time of a handful of non-trivial brainfuck programs. The chart below illustrates the impact of the techniques covered.
Prerequisites
If you’re new to the brainfuck programming language, then head on over to the previous post where we cover both the basics of the language as well as some of the issues encountered when writing a brainfuck-to-java compiler in brainfuck. With that said, most of this post should be grokkable even without prior experience of the language.
Programs worth optimizing
In order to meaningfully evaluate the impact different optimization techniques can have, we need a set of brainfuck programs that are sufficiently non-trivial for optimization to make sense. Unsurprisingly, most brainfuck programs out there are pretty darn trivial, but there are some exceptions. In this post we’ll be looking at six such programs.
The interested reader is encouraged to head over to this repository for a more detailed description of these programs.
An intermediary representation
Our first step is to define an intermediary representation (IR) on which an optimizer can operate. Working with an IR enables optimizations that are platform independent and brings more expressiveness than brainfuck itself. To further illustrate how the IR functions, we’ll also give C implementations for each operation.
In the table below we find all 8 brainfuck instructions, their IR counterparts and an implementation of the IR in C. This basic mapping provides a very simple and somewhat naive way of compiling brainfuck.
| BF | IR | C |
|---|---|---|
+ |
Add |
mem[p]++; |
- |
Sub |
mem[p]--; |
> |
Right |
p++; |
< |
Left |
p--; |
. |
Out |
putchar(mem[p]); |
, |
In |
mem[p] = getchar(); |
[ |
Open |
while(mem[p]) { |
] |
Close |
} |
The C code depends on the memory area and pointer having been set up properly, e.g. like this:
char mem[65536] = {0};
int p = 0;
At this point the IR is no more expressive than brainfuck itself but we will extend it later on.
Making things faster
Throughout the remainder of this post we’ll look at how different optimizations affect the execution time of our 6 sample programs. The brainfuck code is compiled to C code which in turn is compiled with gcc 4.8.2. We use optimization level 0 (-O0) to make sure we benefit as little as possible from gcc’s optimization engine. Run time is then measured as average real time over 10 runs on a Lenovo x240 running Ubuntu Trusty.
Contraction
Brainfuck code is often riddled with long sequences of +,
-, < and >. In our naive
mapping, every single one of these instructions will result in a line
of C code. Consider for instance the following (somewhat contrived)
brainfuck snippet:
+++++[->>>++<<<]>>>.
This program will output an ascii newline character (ascii 10,
‘\n’). The first sequence of + stores the number 5 in the current
cell. After that we have a loop which in each iteration subtracts 1
from the current cell and adds the number 2 to another cell 3 steps to
the right. The loop will run 5 times, so the cell at offset 3 will be
set to 10 (2 times 5). Finally, this cell is printed as output.
Using our naive mapping to C produces the following code:
mem[p]++;
mem[p]++;
mem[p]++;
mem[p]++;
mem[p]++;
while (mem[p]) {
mem[p]--;
p++;
p++;
p++;
mem[p]++;
mem[p]++;
p--;
p--;
p--;
}
p++;
p++;
p++;
putchar(mem[p]);
We can clearly do better. Let’s extend these four IR operations so
that they accept a single argument x indicating that the
operation should be applied x times:
| IR | C |
|---|---|
Add(x) |
mem[p] += x; |
Sub(x) |
mem[p] -= x; |
Right(x) |
p += x; |
Left(x) |
p -= x; |
Out |
putchar(mem[p]); |
In |
mem[p] = getchar(); |
Open |
while(mem[p]) { |
Close |
} |
Applying this to our snippet produces a much more compact piece of C:
mem[p] += 5;
while (mem[p]) {
mem[p] -= 1;
p += 3;
mem[p] += 2;
p -= 3;
}
p += 3;
putchar(mem[p]);
Analyzing the code of our six sample programs is encouraging. For
instance, about 75% of the instructions in factor.b, hanoi.b and
mandelbrot.b are contractable, i.e. part of a sequence of at least 2
immediately adjacent >, +,
< or -. Lingering around 40% we have
dbfi.b and long.b, while awib-0.4.b is at 60%. Still, we shouldn’t
stare ourselves blind at these figures; it could be that these
sequences are only executed rarely. Let’s look at an actual
measurement of the speedup.
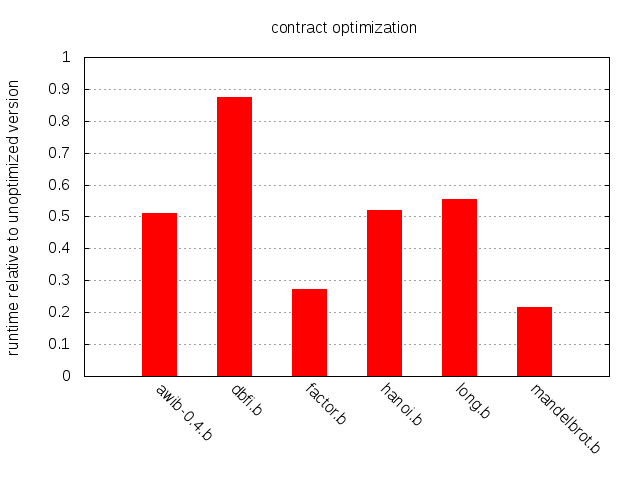
The impact is impressive overall and especially so for mandelbrot.b and factor.b. On the other end of the spectrum we have dbfi.b. All in all, contraction appears to be a straightforward and effective optimization that all brainfuck compilers should consider implementing.
Clear loops
A common idiom in brainfuck is the clear loop: [-]. This
loop subtracts 1 from the current cell and keeps iterating until the
cell reaches zero. Executed naively, the clear loop’s run time is
potentially proportional to the maximum value that a cell can hold
(commonly 255).
We can do better. Let’s introduce a Clear operation to
the IR.
| IR | C |
|---|---|
Add |
mem[p]++; |
Sub |
mem[p]--; |
Right |
p++; |
Left |
p--; |
Out |
putchar(mem[p]); |
In |
mem[p] = getchar(); |
Open |
while(mem[p]) { |
Close |
} |
Clear |
mem[p] = 0; |
In addition to compiling all occurrences of [-] to
Clear, we can also do the same for [+]. This
works since (all sane implementations of) brainfuck’s memory model
provides cells that wrap around to 0 when the max value is exceeded.
Inspecting our sample programs reveals that roughly 8% of the instructions in hanoi.b and long.b are part of a clear loop, while the corresponding figure for the other programs is around 2%.
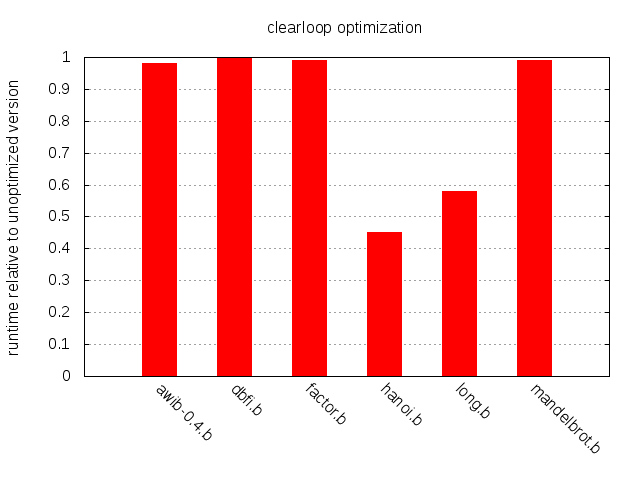
As expected, the impact of the clear loop optimization is modest for all but long.b and hanoi.b, but the speedup for these two is impressive. Conclusion: the clear loop optimization is simple to implement and will in some cases have significant impact. Thumbs up.
Copy loops
Another common construct is the copy loop. Consider for instance this
little snippet: [->+>+<<]. Just like the
clear loop, the body subtracts 1 from the current cell and iterates
until it reaches 0. But there’s a side effect. For each iteration the
body will add 1 to the two cells above the current one, effectively
clearing the current cell while adding its original value to the
other two cells.
Let’s introduce another IR operation called Copy(x) that
adds a copy of the current cell to the cell at offset x.
| IR | C |
|---|---|
Add(x) |
mem[p] += x; |
Sub(x) |
mem[p] -= x; |
Right(x) |
p += x; |
Left(x) |
p -= x; |
Out |
putchar(mem[p]); |
In |
mem[p] = getchar(); |
Open |
while(mem[p]) { |
Close |
} |
Clear |
mem[p] = 0; |
Copy(x) |
mem[p+x] += mem[p]; |
Applying this to our copy loop example ([->+>+<<])
results in three IR operations, Copy(1), Copy(2), Clear,
which in turn compiles into the following C code:
mem[p+1] += mem[p];
mem[p+2] += mem[p];
mem[p] = 0;
This will execute in constant time while the naive implementation of
the loop would iterate as many times as the value held in
mem[p].
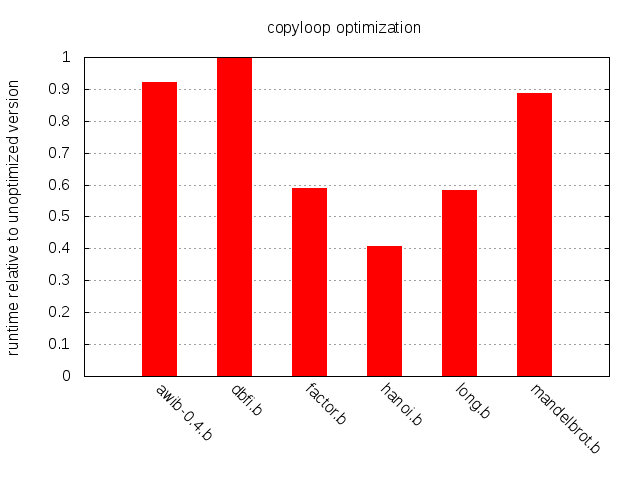
Improvement across the board, except for dbfi.b.
Multiplication loops
Continuing in the same vein, copy loops can be generalized into
multiplication loops. A piece of brainfuck like
[->+++>+++++++<<] behaves a bit like an
ordinary copy loop, but introduces a multiplicative factor to the
copies of the current cell. It could be compiled into this:
mem[p+1] += mem[p] * 3;
mem[p+2] += mem[p] * 7;
mem[p] = 0
Let’s replace the Copy operation with a more general
Mul operation and have a look at what it does to our
sample programs.
| IR | C |
|---|---|
Add(x) |
mem[p] += x; |
Sub(x) |
mem[p] -= x; |
Right(x) |
p += x; |
Left(x) |
p -= x; |
Out |
putchar(mem[p]); |
In |
mem[p] = getchar(); |
Open |
while(mem[p]) { |
Close |
} |
Clear |
mem[p] = 0; |
Mul(x, y) |
mem[p+x] += mem[p] * y; |
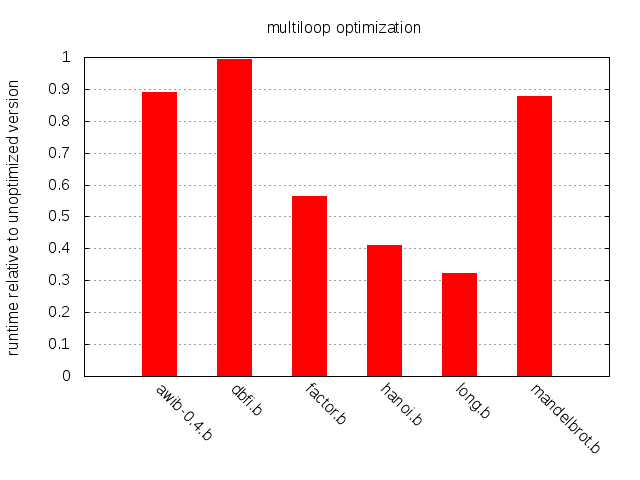
While most programs benefit slightly from the shift from
Copy to Mul, long.b improves significantly
and hanoi.b not at all. The explanation is simple: long.b
contains no copy loops but one deeply nested multiplication loop;
hanoi.b has no multiplication loops but many copy loops.
Scan loops
We have so far been able to improve the performance of most of our
sample programs, but dbfi.b remains elusive. Examining the source code
reveals something interesting: out of dbfi.b’s 429 instructions, a
whopping 8% can be found in loops like [<] and
[>]. Contrast that with awib-0.4 being at 0.8% and the
other programs having no occurrences of this construct at all. These
pieces of code operate by repeatedly moving the pointer (left or
right, respectively) until a zero cell is reached. We saw a nice
example in the
previous post of how they can be utilized.
It should be mentioned that while scanning past runs of non-zero cells
is a common and important use case for these loops, it is not the only
one. For instance, the same construct can appear in snippets like
+<[>-]>[>]<, the exact meaning of which is
left as an exercise for the reader to figure out. With that said, the
scanning case can be very time consuming when traversing large memory
areas and is arguably what we should optimize for.
Fortunately for us, the problem of efficiently searching a memory area
for occurrences of a particular byte is mostly solved by the C
standard library’s memchr() function. Scanning
“backwards” is in turn handled by the GNU extension
memrchr(). In a nutshell, these functions operate by
loading full memory words (typically 32 or 64 bits) into a CPU
register and checking the individual 8-bit components in
parallel. This proves to be much more efficient than loading and
inspecting bytes one at a time.
Let’s extend the IR by adding two new operations:
ScanLeft and ScanRight.
| IR | C |
|---|---|
Add(x) |
mem[p] += x; |
Sub(x) |
mem[p] -= x; |
Right(x) |
p += x; |
Left(x) |
p -= x; |
Out |
putchar(mem[p]); |
In |
mem[p] = getchar(); |
Open |
while(mem[p]) { |
Close |
} |
Clear |
mem[p] = 0; |
Mul(x, y) |
mem[p+x] += mem[p] * y; |
ScanLeft |
p -= (long)((void *)(mem + p) - memrchr(mem, 0, p + 1)); |
ScanRight |
p += (long)(memchr(mem + p, 0, sizeof(mem)) - (void *)(mem + p)); |
An unfortunate consequence of using array indexes instead of direct pointer manipulation is that the C versions of the scan operations look pretty horrid. Well, such is life.
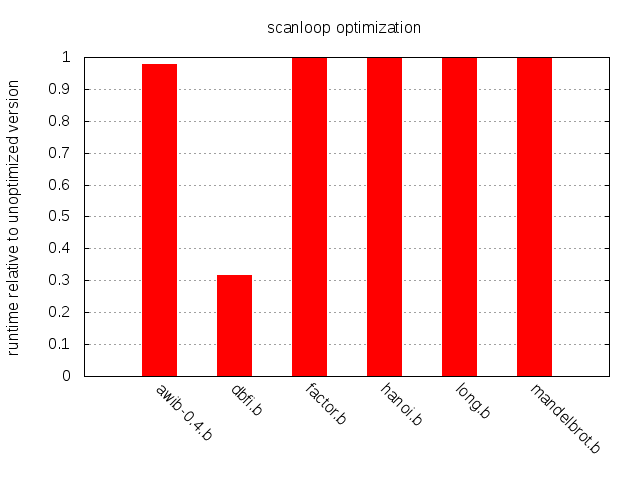
More than a 3x speedup for dbfi.b while the other programs see little
to no improvement. There is of course no guarantee that
memchr() will perform as well on other libc
implementations or on a different architecture, but there are
efficient and portable memchr() and
memrchr() implementations out there so these functions
can easily be bundled by a compiler.
Operation offsets
Both the copy loop and multiplication loop optimizations share an
interesting trait: they perform an arithmetic operation at an offset
from the current cell. In brainfuck we often find long sequences of
non-loop operations and these sequences typically contain a fair
number of < and >. Why waste time
moving the pointer around? What if we precalculate offsets for the
non-loop instructions and only update the pointer at the end of these
sequences?
| IR | C |
|---|---|
Add(x, off) |
mem[p+off] += x; |
Sub(x, off) |
mem[p+off] -= x; |
Right(x) |
p += x; |
Left(x) |
p -= x; |
Out(off) |
putchar(mem[p+off]); |
In(off) |
mem[p+off] = getchar(); |
Clear(off) |
mem[p+off] = 0; |
Mul(x, y, off) |
mem[p+x+off] += mem[p+off] * y; |
ScanLeft |
p -= (long)((void *)(mem + p) - memrchr(mem, 0, p + 1)); |
ScanRight |
p += (long)(memchr(mem + p, 0, sizeof(mem)) - (void *)(mem + p)); |
Note that while Clear and Mul are included
in this table, the test was run with the operation offset optimization
in isolation, so these two operations were never emitted by the
compiler.
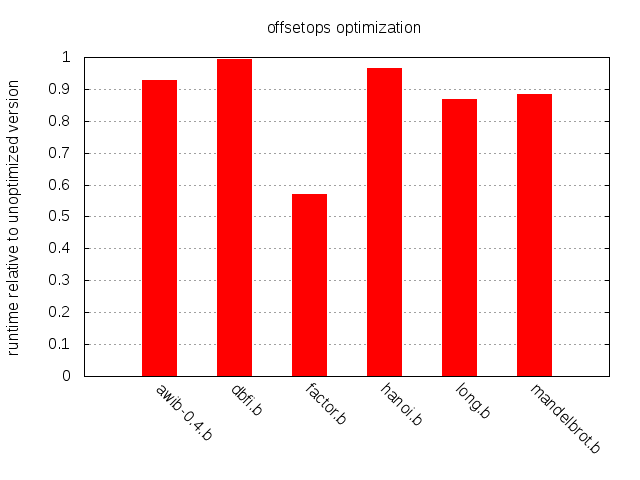
Tangible results, albeit somewhat meager.
Applying all optimizations
To wrap up, let’s have a look at what we can accomplish by applying all these optimizations to our sample programs.
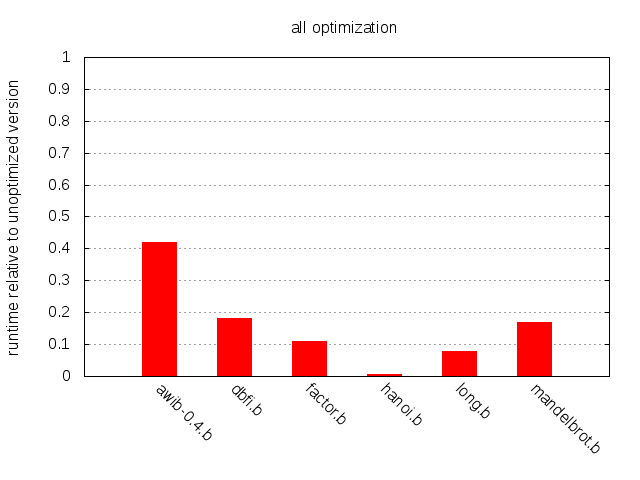
Significant improvement across the board, ranging from about 130x in the case of hanoi.b to the 2.4x speedup of awib-0.4.
Summary
Fairly simple techniques proved to significantly improve the performance of our sample programs. Brainfuck compiler writers should consider implementing at least some of them. Now, spending time and effort on such an esoteric language as brainfuck may seem like a pointless exercise, but we hope and believe that some of the concepts can carry over to more real settings. Also, mucking around with brainfuck is just plain fun.
That was all.
See also: Discussion on hacker news